1. 개요

순환 루프를 가지지 않는 연결된 유향(방향이 있는) 그래프이다. 연결된 두 개의 노드는 부모-자식 관계로 정의되고, 부모에서 자식으로 간선의 방향성을 가진다.

이처럼 트리는 부모-자식이라는 선후관계에 따라 계층적 자료구조(Hierarchical Data Structure) 정의된다.

1.1. 특징

하나의 노드에 대해 여러개의 노드가 이어지는 비선형 자료구조이다.
트리구조 내에 또 다른 트리구조를 가지는 있는 재귀적 자료구조이다.
노드가 n개인 트리는 node-1개의 간선을 가진다.
임의의 어떤 어떤 두 정점을 잡아도 단순 경로가 단 하나 존재한다.
어떤 간선을 제거해도 연결 그래프가 아니게 된다.

1.2. 용어

노드 (node)
트리를 구성하는 기본 원소
- 루트 노드 (root node)
  부모가 없는 최상위 노드
- 부모 노드 (parent node)
  루트 노드 방향으로 직접 연결된 노드
- 자식 노드 (child node)
  루트 노드 반대방향으로 직접 연결된 노드
- 형제 노드 (siblings node)
  같은 부모 노드를 가지는 다른 노드
- 내부 노드 (leaf node)
  자식 노드가 있는 노드
- 리프 노드 (leaf node)
  자식 노드가 없는 노드
간선(edge) 노드와 노드 간의 연결선
경로(path)
두 노드 사이 노드들의 순서
크기(size)
노드의 갯수
레벨, 깊이(level, depth)
특정 노드와 루트 노드 사이의 간선 갯수
높이(height)
트리의 최대 깊이
너비(width)
특정 레벨에 있는 노드의 갯수
차수(degree)
특정 노드의 자식 노드 갯수

2. Binary Tree

2.1 개요

자식 노드 개수(차수)를 최대 2개로 제한하는 트리

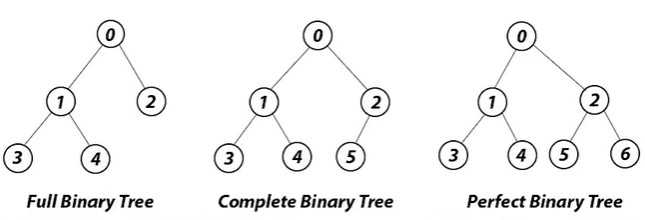
정 이진 트리(Full Binary Tree)
모든 노드의 차수가 0 혹은 2인 이진트리. 즉, 리프 노드를 제외한 모든 노드들이 2개의 자식을 가진다.
완전 이진 트리(Complete Binary Tree)
리프 노드의 높이 차가 최대 1이고, 오른쪽 자식 노드가 있으면 반드시 왼쪽 자식이 있는 이진트리이다. 즉, 노드를 트리의 상단 왼쪽부터 채워나간 이진트리
포화 이진 트리(Perfect Binary Tree)
리프 노드들이 모두 같은 레벨이 있는 이진트리.

2.2. 순회

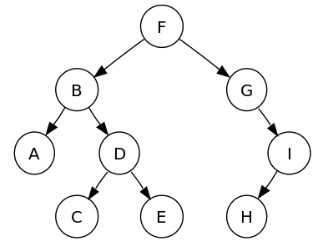
전위 순회: F, B, A, D, C, E, G, I, H
중위 순회: A, B, C, D, E, F, G, H, I
후위 순회: A, C, E, D, B, H, I, G, F
레벨 순회: F, B, G, A, D, I, C, E, H

2.2.1. 전위 순회 (preorder)

깊이 우선 탐색(depth-first-traversal)이라고도 한다.

노드를 방문한다.
왼쪽 서브 트리를 전위 순회한다.
오른쪽 서브 트리를 전위 순회한다.

2.2.2. 중위 순회 (inorder)

왼쪽 서브 트리를 중위 순회한다.
노드를 방문한다.
오른쪽 서브 트리를 중위 순회한다.

2.2.3. 후위 순회 (postorder)

왼쪽 서브 트리를 후위 순회한다.
오른쪽 서브 트리를 후위 순회한다.
노드를 방문한다.

2.2.4. 레벨 순서 순회 (level-order)

너비 우선 탐색(breadth-first-traversal)이라고도 한다.

낮은 레벨의 왼쪽부터 순회한다.

2.3. 구현

Python

# 노드
class Node:
    def __init__(self, item):
        self.item = item  # 노드의 값
        self.left = None  # 왼쪽 자식 노드
        self.right = None # 오른쪽 자식 노드

# 이진 트리
class BinaryTree():
    # 생성자
    def __init__(self, root = None):
        self.root = root  # 루트 노드

    # 전위 순회
    def preorder(self, node):
        if node != None:
            print(node.item, end=' ') # 노드 방문
            if node.left:
                self.preorder(node.left) # 왼쪽 서브트리 전위 순회
            if node.right:
                self.preorder(node.right) # 오른쪽 서브트리 전위 순회

    # 후위 순회
    def postorder(self, node):
        if node != None:
            if node.left:
                self.postorder(node.left) # 왼쪽 서브트리 후위 순회
            if node.right:
                self.postorder(node.right) # 오른쪽 서브트리 후위 순회
            print(node.item, end=' ') # 노드 방문

    # 중위 순회
    def inorder(self, node):
        if node != None:
            if node.left:
                self.inorder(node.left) # 왼쪽 서브트리 중위 순회
            print(node.item, '', end='') # 노드 방문
            if node.right:
                self.inorder(node.right) # 오른쪽 서브트리 중위 순회

    # 레벨 순회 (BFS)
    def levelorder(self, node):
        q = []
        q.append(node)
        while q:
            node = q.pop(0)
            print(node.item, '', end='')
            if node.left != None:
                q.append(node.left)
            if node.right != None:
                q.append(node.right)

2.5. 활용

Binary Search Tree (Data Structure)
Heap (Data Structure)
Huffan's Code (Greedy Algoritm)
백준 2263번 트리의 순회
중위 순회 + 후위 순회 -> 전위 순회
백준 4256번 트리
전위 순회 + 중위 순회 -> 후위 순회

3. 활용

Tree (Greedy Algoritm)

트리(Tree) 자료구조